MSRA：视觉生成六大技术问题

文生图、文生视频，视觉生成赛道火热，但仍存在亟需解决的问题。

微软亚洲研究院研究员古纾旸对此进行了梳理，他认为视觉信号拆分是最本质的问题。

生成模型的目标是拟合目标数据分布，然而，目标数据分布过于复杂，难以直接拟合。
因此，往往需要将复杂的信号做拆分，拆分成多个简单的分布拟合问题，再分别求解。信号拆分方式的不同产生了不同的生成模型。

此外，针对一些热点问题他也展开进行了分析，一共六大问题，例如diffusion模型是否是最大似然模型？diffusion模型的scaling law是什么样的？

以下是部分问题的具体讨论。

视觉信号拆分问题

为什么大语言模型能这么成功？

作者认为，最本质的原因是文本信号拆分具有“等变性”。

具体来说，对于一个文本序列A=x0,x1,x2…语言模型会根据位置把P(x0,x1,x2…)的联合数据分布拆分成多个条件概率分布拟合问题：

P(x0),P(x1|x0),P(x2|x0,x1)…对于一个文本，比如说“我喜欢打篮球”，用自回归的方式进行拟合，那么对于从“打”回归“篮球”这个子任务，和它是文本中的第几个词没有关系。

也就是说，不论对于第一个任务P(x1|x0)还是第三个任务P(x3|x0,x1,x2)，要拟合分布的其实是“一致”的，或者叫“等变”的。

因此，可以利用一个模型，同时去解决这些相关性很高的任务。

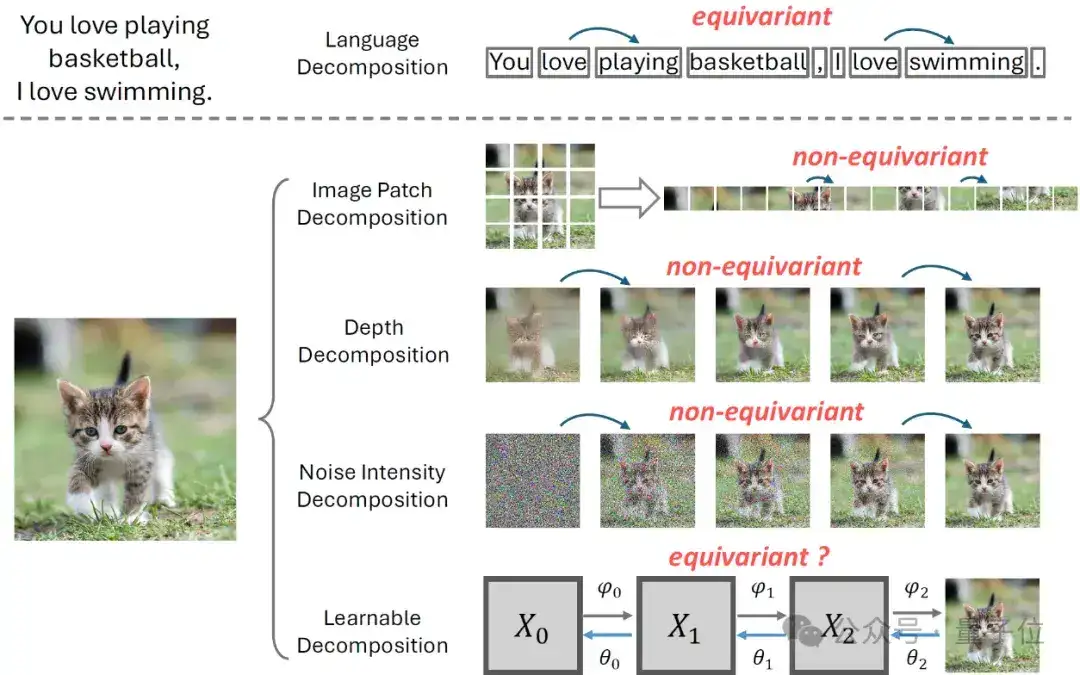
然而对于图像信号，目前常见的拆分方式包括：图像块拆分，深度拆分，噪声强度拆分，以及可学习拆分。这些拆分方式都不能保证是“等变的”（equivariant）。

图像块拆分将图像根据空间位置分成图像块，后面的图像块根据前面的进行生成，代表性的工作有iGPT、DALL-E等。

然而图像不同位置有独立的inductive bias，具体来说，虽然单行的块内具有连续性，但是一行的最后一个块与下一行的第一个块之间却缺乏这种连续性。

再比如对于人脸数据集，人脸大多出现在图像的中间位置，而不是图像边缘。这些都说明了，根据空间位置来进行划分，不同任务学习目标有差异，不具备“等变性”。

深度拆分的代表性工作包括VQVAE2、RQVAE等。一般遵循coarse-to-fine的方式进行生成，前期拟合低频信号，后期拟合高频信号。因此，这个学习目标的不同也导致了缺乏“等变性”。

此外，这类方法还可能导致“无效编码”问题，将在后文介绍。

扩散模型根据噪声强度对图像信号进行拆分。对于数据集中的图像x0，将其加噪成一个序列x0,x1,x2,…xN，其中xN几乎是纯噪声，生成过程其实是在解决N个去噪任务：P（xt|xt+1）。

然而，之前的工作（MinSNR、eDiff-I）发现尽管都是去噪任务，但是不同噪声强度的去噪任务仍然有很大的差异，不具备“等变性”。

最后一类是可学习的拆分方式。代表性工作包括VDM、DSB等等。这类想法大多基于扩散模型的噪声强度拆分，不过加噪过程是学习得到的，而不是提前的定义好的。

其中VDM学习加噪过程中的参数，DSB通过一个网络来学习如何加噪。然而，这些工作目前只是有潜力保证“等变性”，在实践中尚未成功。此外，他们目前仍然存在一些挑战（参见SDSB）。

“不等变性”导致的问题是：既然各个任务有冲突，那博鱼·综合体育用不用共享参数的模型来拟合这些分布呢？

如果用，那共享参数的模型很难同时拟合这些目标有差异的任务，如果不用，会导致模型的参数量爆炸，实际不可行。目前实践中可能会同时使用多种信号拆分方式来简化分布复杂度，然而该做法依旧是“非等变”的。

基于图像信号拆解的“非等变性”，会引发一系列问题。文章的后续章节讨论的问题和图像拆解的“等变性”都息息相关。下面将简单进行介绍。

Tokenization问题

如果采用RQVAE进行编码，很容易出现当编码长度比较长的时候，后续的编码不能帮助提升重建质量，甚至对重建质量有损害的问题。

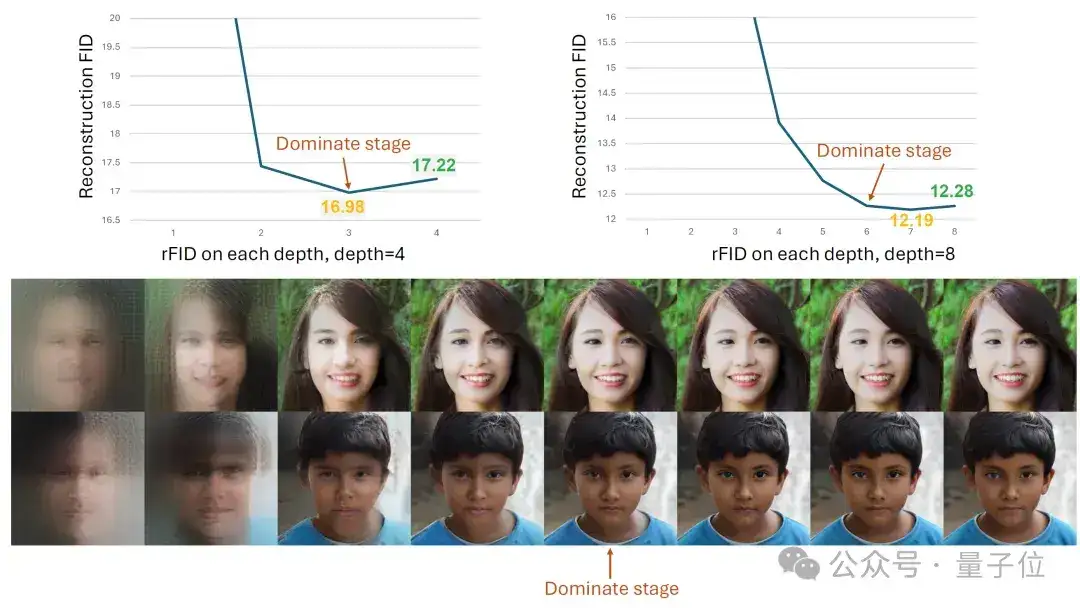
作者通过一定的数学简化，对该问题提供了一个直观的解释，分析了该问题出现的原因。

让D代表解码器，I代表原始输入图像。不同深度的编码由x0,x1,x2,…xN表示，其中N是编码的深度在本例中假设为4。

因此，RQVAE的重构损失L可以被认为是以下四个重构损失的组合：

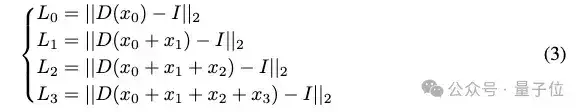
为了简化分析，提出两个假设。首先，假定解码器执行线性变换，以便更简单地分析结果。其次，按照常规配置，对四种损失赋予相同的权重。基于这些假设，可以按以下方式简化重构损失的计算：

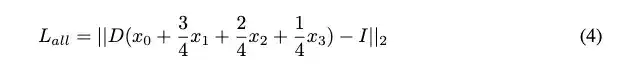
因此，最小化图像级重构损失的潜在空间表示将是：

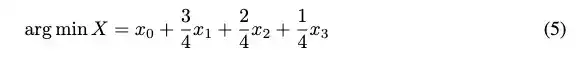
这不能保证x0+x1+x2+x3比x0+x1+x2更接近arg min X。假设不同深度的编码共享一个通用代码本，并独立同分布，那么后者肯定比前者更接近理论最小值。

因此，这导致了无效编码问题。

扩散模型是最大似然模型吗？

尽管DDPM从最大似然的角度出发，推导了扩散模型的理论。然而，有很多发现似乎表明，扩散模型并非最大似然模型。

VDM++证明了，当不同噪声强度处的损失函数权重满足单调关系时，扩散模型是最大似然模型。然而，实际训练中，往往并不采用这样的损失函数权重。

在测试阶段，Classifier-free guidance的采用也使得优化目标不再是最大似然。在评估阶段，直接用NLL损失作为衡量指标，并不能准确评估生成模型的好坏。

这都引出了一个问题：为什么最大似然的方法并不能获得最优的结果？

针对该问题，作者从“等变性”的角度，给出了一种理解方式。

得分匹配与非规范化最大似然密切相关。通常，得分匹配可以避免最大似然学习中学到的所有数据点的等概率的倾向。对于某些特殊分布，如多元高斯分布，得分匹配和最大似然是等价的。

VDM++的研究表明，使用单调损失权重ω(t)实际上等同于为所有中间状态最大化ELBO。然而，单调权重并不能表征不同噪声强度任务的训练难度差异。

如前所述，图像数据通常不具备这种等变性。在实际训练中，学习似然函数的难度随噪声强度变化；直观上，最大的困难出现在中等噪声水平，在这里似然函数往往学习得不够准确。在生成过程中，使用无分类器引导可以看作对学习不佳的似然函数的矫正。

在模型评估过程中，鉴于不同噪声水平的任务对最终结果的重要性不同，对这些NLL损失应用相同权重无法有效衡量最终生成输出的质量。

怎么平衡扩散模型中不同噪声步间的冲突？

从VDM++的训练损失出发：

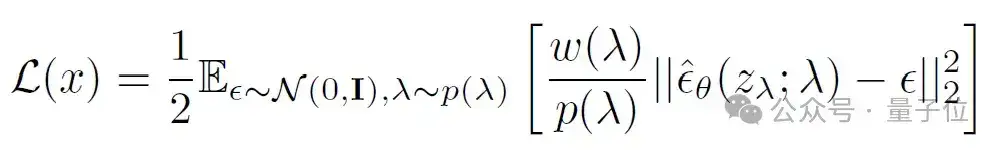
要调节训练过程中不同噪声强度的冲突，要不改变损失函数ω (λ)，要不改变采样频率P(λ)。

理论上两者是等价的，然而实际训练过程中，改ω (λ)变相当于改变learning rate，改变P(λ)相当于给更重要的任务提供了更大的采样频率，增多了这部分任务的计算量(Flops)，这往往比改变损失函数更有效。

最近的工作“Improved Noise Schedule for Diffusion Training”，经验性地给出了一种解决方案。

扩散模型存在scaling law吗？

大语言模型的成功很大程度上归功于scaling law。对于扩散模型，存在scaling law吗？

这个问题的关键在于采用什么指标来评估模型质量的好坏。在这里分析了三种做法：

1、用“Improved Noise Schedule for Diffusion Training”中的不同任务的难度系数当重要性系数，给不同任务的损失加权，当成衡量指标。对模型参数量，训练迭代次数和最终性能的关系分别建模，可以得到下面的结果。然而，该指标不能确保与人类的偏好完全一致。

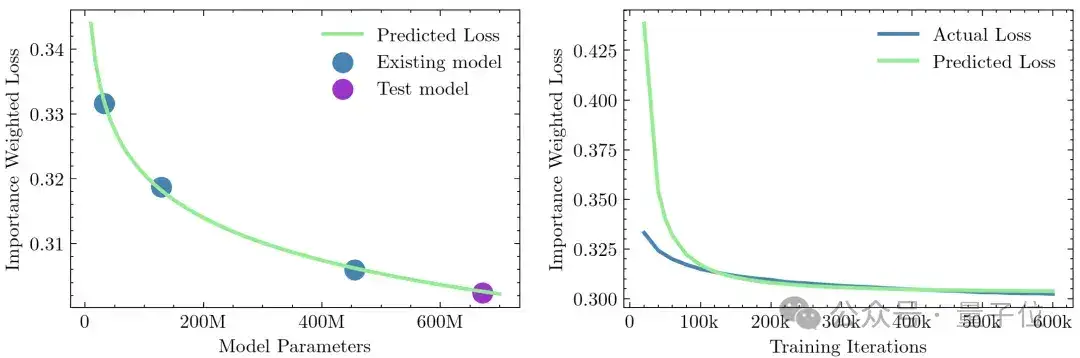
2、利用已有的生成模型衡量指标，如FID等。这类方法有两个问题，第一，FID等指标自身的bias，比如FID假设图像抽取特征后的分布满足高斯分布，这会带来系统误差。第二，该指标一般用于衡量生成数据分布和目标分布之间的差异，这在in-the-wild场景下和人类偏好可能会有差异。

3、直接采用人工标注衡量模型质量。收集好大量文本-图像数据，用生成模型从这些文本生成图像，并让用户评估生成结果和ground truth的偏好度，该指标可以作为模型scaling law的衡量指标。这种做法的缺点是需要大量人力，但是可以对齐生成结果和人类偏好。此外，该指标可以指导测试方法的选择。

原文链接：https://cientgu.github.io/files/VisualSignalDecomposition.pdf

— 完 —